POWER & REVERSIBILITY

• Energy and Power
Time plays no role in much of thermodynamics as it is typically taught in physics and chemistry classes. The focus in such classes is on equilibrium states and processes that connect them. The time taken by the process is often irrelevant to the analysis and is not broached. In real-life processes, the situation is very different. On a hot summer day, some of the dials on an electric meter rotate rapidly, signifying that energy is being used more rapidly than when it is cooler outside and the dials are moving more slowly.
The rate at which electrical energy is being transformed, measured in joules/second, is called power. The formula is simple:
![]()
It follows that the units are joules/second. The concept of power is sufficiently important and commonly used that 1 joule/second is given its own name, the watt. This name arose in part because in 1782, James Watt studied power and determined how many times a horse could turn a milling wheel in an hour, which led to the concept of one horsepower. In the old system of British units, which used foot-pounds as a unit of work (recall that work = force x displacement), one horsepower was defined as 33000 foot-pounds/minute. In the currently-used System of International Units (SI), one horsepower = 746 watts.
It has been my experience that students have great difficulty distinguishing between the concepts of energy and power. It sometimes helps to examine examples where power is high, but energy is small, and vice versa. Suppose a 1000 megawatt electric-generating plant operates for one nanosecond = 10-9 seconds. The power during that operation is 109 watts—relatively large on a human scale—while the energy transformed is 109 x 10-9 = 1 joule—relatively small, say, relative to the Calorie (1 Calorie = 4186 joules).
The opposite result, large energy but low power, occurs for an envisaged relatively dim 5 watt light bulb that operates for 50 years (unlikely in real life, but a helpful example), transforming the substantial 1.58 x 109 joules (=337,449 Calories) of energy at the relatively low power of 5 watts.
On a human scale, a person who processes sufficient food to transform 2000 Calories = 8.37 x 106 joules in 24 hours (8.64 x 104) seconds, has an average power of
Average Power = 8.37 x 106 joules/8.64 x 104 seconds = 97 watts.
That is, humans transform energy at a rate similar to that of a 100 watt incandescent light bulb. However, the bulb's filament has a tiny surface area from which to spread energy to the surroundings, and only by doing so will its temperature not rise uncontrollably. The electromagnetic radiation rate is proportional to temperature to the fourth power, and filament temperatures must rise to about 2800 kelvins (2500°C) in order to not get hotter. In contrast, a human has a relatively large surface area, and operates at a temperature of about 300 kelvins (= 37 °C). Our combination of surface area and temperature are sufficient to keep our body temperatures from rising under normal circumstances.
What operates at relatively low power? "Low" is a relative term. Compared to the power levels cited above, an electric wristwatch has a "low" power of about 10-6 watts. The best FM tuners can pick up signals at about 10-15 watts!
At the higher end of the power spectrum there is the average power of all living humans and their technology, about 15 x 1012 watts, the rate at which energy is being transformed from one form to another. Considerably higher is the luminosity of the Milky Way galaxy, which is estimated to be about 5 x 1036 watts.
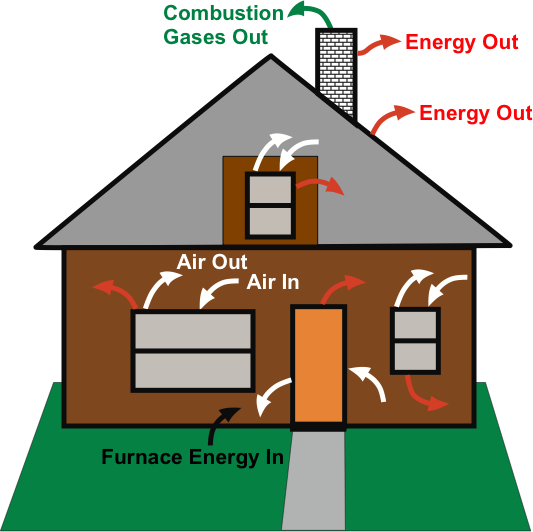
What relevance does power have to thermodynamics? Suppose you want to heat a home to 25 °C when the outdoor temperature is 0 °C. The figure depicts the home, with colored arrows indicating some of the energy and matter gains and losses. Air infiltration and exfiltration, which are primarily at windows and doors, are denoted by white arrows. Energy losses that occur because the inside of the house is warmer than the outside air, are shown with red arrows. Combusion gases leaving the chimney are indicated in green. Good insulation can cut down the energy losses significantly, and good door and window seals can cut down on the air infiltration and exfiltration. Highly efficient furnaces minimize the energy carried away in the combustion products.
Why are power considerations relevant in this example? Energy is lost at a given rate by heat processes through the buildings envelope, namely, walls, roof and floor. Energy is also lost by infiltration of cold outdoor air and exfiltration of warmer indoor air. In order to keep the indoor temperature at the desired setting, the rate at which heating is accomplished by the furnace must balance the rate at which energy is lost through the envelope.
Furnace heating rate = Energy loss rate from heat processes and air flow
Furnaces are rated according to their heating rates. In the United States, these rates are given in units Btu/hour. For a 1600-2000 square ft. house, a typical furnace rating is 80000 Btu/hour, which is equivalent to 23400 watts = 23.4 kilowatts (kW).
You might be familiar with portable electric heaters, which are also rated in watts or kilowatts. These operate by passing electric current through a metal resistor, which heats up and radiates energy to the surroundings. Those that are powered by connection to a 120 volt electric line, with a (common) 15 ampere circuit breaker, are limited to 1800 watts. This is because the power level of the energy transformation in an electric resistor is given by
Power = voltage x current
The units work out because 1 volt = 1 joule/coulomb (energy per unit charge) and 1 ampere = 1 coulomb/sec, so 1 volt x 1 amp = 1 joule/second = 1 amp.
Some electric heaters advertise that they heat more efficiently than others. In actual fact, two different heaters each operating at 1800 watts provide the same energy to the surroundings over the same time interval. They might deliver the energy differently, e.g., from a larger surface area or using cleverly designed natural convection, but neither heats more than the other.
A portable heater has the big advantage of being able to heat only occupied rooms, rather than all rooms of a home. Nevertheless, the stark fact is that if a room loses energy at a rate of 1600 watts, a 600 watt "efficient" heater cannot supply energy fast enough to keep the temperature from dropping. Such units can however heat a nearby area, keeping it warmer than the average room temperature. That is true for any electric heater.
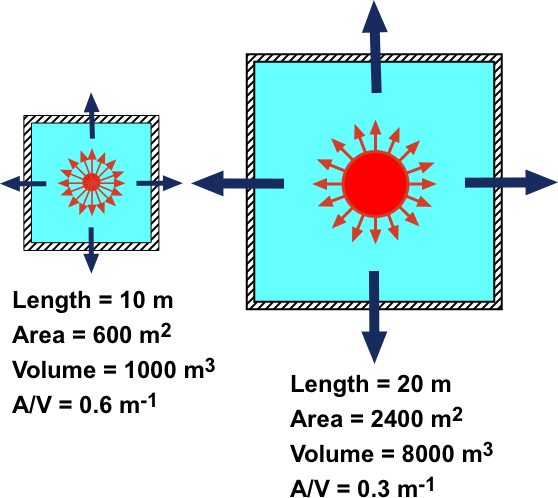
The rate of energy loss by heat processes through the envelope is roughly proportional to the surface area A of that envelope and the temperature difference between indoor and outdoor temperature, and inversely proportional to the thermal resistance R. It is written,
![]()
Typical R values in cold climate areas is 19 ft2-°F/(Btu/hour) = 3.35 m2-kelvin/watt. For a cubical room 10 m x 10 m x 10 m, with A = 600 m2 and an indoor-outdoor temperature difference = 25 K (45 °F) we find an energy loss rate of 4478 watts. This would require three 1800 watt electric heaters to heat it.
Note that the energy loss rate through the envelope area A depends only on A and not on the volume of the room. Comparing a cubical room with one that has twice its linear dimensions, the volume of the larger room is eight times larger than that of the smaller room, as shown in the figure. However the envelope's area is only 4 times larger than that of the smaller one. It follows that the energy loss rate through the larger room's envelope is four times greater than that for the smaller room.
In contrast, if one sets back the thermostat, or turns off the heating system for a number of hours, heating the room depends directly on both the volume of air in the room and the amount and type of furniture. This is because the air and every object in the room will have cooled and must be heated back up to normal room temperature. Heating the air in the larger room will take eight times the energy of the smaller room and, assuming the furniture pretty much fills the floor space, that will take only four times the energy of the smaller room. This behavior is a result of the reduced surface-to-volume ratio of the larger room relative to the smaller one.
It is common for larger buildings to stay warmer in winter because they have smaller surface-to-volume ratios. The rate at which they cool depends inversely on the volume of stuff being cooled, but is directly proportional to the envelope's area. That is, the rate of cooling is proportional to the surface-to-volume ratio.
What is true for buildings is also true, at least approximately, for people. Larger people often are comfortable wearing short-sleeved shirts in winter, while smaller people tend to wear long sleeves and/or sweaters. Clearly, surface-to-volume ratios can be very important in heat processes.
We have seen that the power requirement of a furnace is dictated by the energy loss rate from heat processes and air infiltration and exfiltration. If such losses could be reduced, required furnace powers could be reduced accordingly. One can envisage an ideal situation where the energy losses through walls have been brought nearly to zero, and the only air flow is the minimum needed to assure a healthy breathing environment—with incoming air being heated by outgoing air using a so-called counterflow heat exchanger. This reduces the degree of irreversibility markedly.
Most energy tasks in our personal lives and in manufacturing plants and other industrial operations can be characterized as being one or a combination of the following energy services. Devices that provide these services can be powered by electricity, a fossil fuel, biofuel, or solar or wind source. Each requires power levels dictated by the user's needs, and each entails irreversible processes.
Mechanical work. Examples are lifting, digging, drilling, cutting, and moving.
Electrical work. This term is most useful for tasks where electrical work is the fundamental goal, as opposed to situations where electrical work is secondary to the main goal. For example, an automobile battery does electrical work to get a starting motor turning. Electrical work is its main task. In contrast, the starting motor starts the engine via mechanical work. Other examples where electrical work is a major goal are: electroplating of metals, electrolysis, and electrolytic reduction of alumina (aluminum oxide) to molten (primary) aluminum. The latter is a particularly energy intensive process, which is why aluminum is recycled.
Heating. Heating of air is done for personal comfort, while heating of water might be for cooking or for a large-scale electric generating plant. Heating of iron ore is done in a blast furnace to separate the iron, and heating is used to manufacture glass, for grain drying bins; and for a host of other industrial processes.
Cooling. Space cooling and food preservation are major examples, but it is used also for freeze drying and other industrial processes. Cooling to extremely low temperatures—near absolute zero—is common and essential in MRI machines.
Lighting. Street lights, home and office illumination, and automobile and other vehicle lights come to mind.
Electronics, opto-electronics and information processing. These services have become a central part of our lives, encompassing video and audio equipment, fiber optic communication, computers, printers and copiers, telephones, automobiles, airplanes, and just about every modern electrical device. Electronics can be, and is, used to control any of the above task types.
Combinations. Many appliances incorporate two or more of the above energy tasks. For example, a clothes dryer has an electric motor that generates mechanical work, accomplishes heating via natural gas combustion, is controlled by an electronics module, and provides a lighted display. Another example is an automobile, which uses mechanical work in many ways. It is started by a battery doing electrical work to power an electric motor that turns the crankshaft, has an air conditioner to provide space cooling and a heater to provide space heating. Additionally, an auto has electronic ignition and other electronic control devices, and uses both interior and exterior lighting.
The main points that emerge from this discussion are: (i) each of the above entails thermodynamics and irreversible processes, with energy being spread to air, nearby material, with some being radiated to outer space; and (ii) each has a power requirement determined either by external conditions—e.g., outdoor temperature—or user needs. In thermodynamics, it is very helpful to consider idealized reversible processes. This limiting case is important to establish efficiencies for heat engines and to do calculations of "state functions." For example, the entropy change between two given equilibrium states A and B is the same for a reversible process as for an irreversible one. This is because the entropy values, SA and SB, in the two states depends only on those states and not on the process used to reach them.
To illustrate reversibility, or more precisely, how reversibility can be approached, I now present three examples: (i) quick piston action to change the volume of a gas, (ii) a heat process that takes a system from one temperature to another, and (iii) a radiating incandescent light bulb.
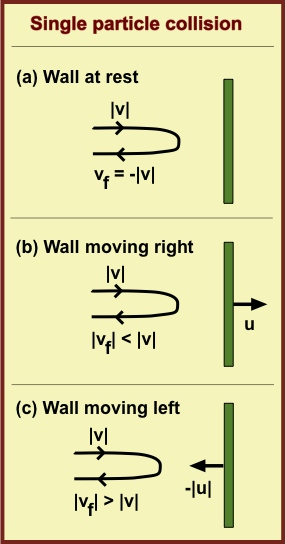
A gas consists of an enormous number of molecules moving in many directions. In any small time interval, say one microsecond the number of collisions on each square centimeter of container wall is typically of order 1023 per second. As illustrated in Fig. (a), each collision reverses the particle's velocity component perpendicular to the wall. That is, the velocity vf after the collision is the negative of that before the collision: vf = -|v|. This also reverses that component of momentum (i.e., particle mass x velocity). Such a momentum change requires a force, in this case provided by the wall. Consistent with Newton's third law, the force of the wall on a particle is accompanied by an equal and opposite force by the particle on the wall. In thermodynamic equilibrium, the fluctuations in this force are small relative to the force magnitudes themselves and this enables us to speak confidently about the pressure—i.e., the force per unit area—on a container wall.
Now suppose the wall is moved at speed u away from the container's interior, as in Fig. (b). How does this affect the force on the wall? It is clear that if the speed u exceeds the particle's speed, there will be no collision and the force will be zero. For a specific smaller speed u there will be only a slight collision and the force will be smaller than when u = 0. That is |vf| < |v|. Indeed when the wall recedes from the particle the relative velocity between wall and particle declines relative to that for a wall at rest. Generally, the force magnitude drops with increasing speed.
If instead the wall is moved toward the oncoming particle as in Fig. (c), the final speed exceeds the initial speed, |vf| > |v|, and the force of the collision will exceed that for a stationary wall. This is why a baseball batter swings the bat as quickly as possible toward the pitched ball. In this case, the relative velocity between wall and particle is greater than for the stationary wall (envisage a head-on collision). Generally, the force magnitude increases with increasing wall (or bat) speed.

Such quick-moving piston actions are irreversible processes because starting with a quick expansion, the gas expands, losing little energy via collisions with the piston. As illustrated, if a rapid compression reduces the volume by ∆V of a well insulated gas and a subsequent rapid expansion returns the system to its original volume, the gas is left with its original volume, but with higher energy and temperature. That is, the two-step process is irreversible.
Similarly, if a quick expansion by ∆V is followed by a quick compression, returning the gas to its initial volume, the gas has higher energy and temperature than it did originally. Thus, for rapid compression followed by rapid expansion or rapid expansion followed by rapid compression, the work by the external force of compression exceeds the work done on the movable wall during the quick expansion. Rapid expansion and compression are irreversible processes.
The effects of irreversibility get smaller as the piston is moved ever more slowly. Indeed it is possible to move the piston so slowly that an expansion that changes the volume by ∆V, followed by a similarly slow compression back to the original volume, brings that gas back to its initial temperature within the limits of our thermometer's resolving power! Therefore, it is common to envisage thought experiments that entail infinitely slow piston motions that are reversible. Such "Gedanken" (thought) experiments are useful conceptually despite the fact that they cannot be executed in a laboratory. We humans don't have time to wait for an infinitely slow process to be completed!
Such idealizations are useful mathematically because calculations can be made along reversible paths that cannot be done along irreversible ones. A main reason is that along an irreversible path, there are generally spatial variations of temperature and pressure. These variations and their changes over time and can be exceedingly complex and difficult to follow mathematically, even using high speed computers.
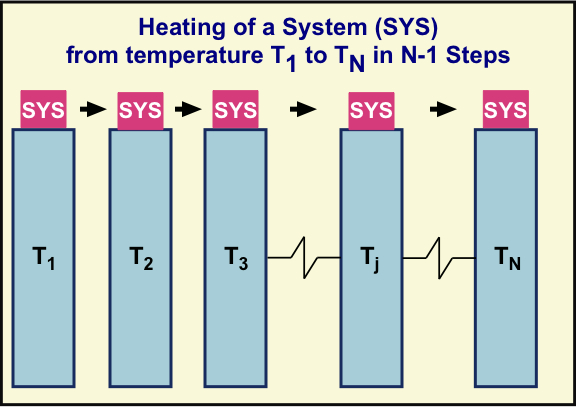
Just as a work process on a gas done by moving a container wall is irreversible, so is an energy transfer induced by a change in temperature. An example is the heating of water in a pot on an electric range. As you might expect, the larger the difference in temperature, the greater the degree of irreversibility. If we can accomplish a temperature change using a succession of individual heating processes through a much smaller temperature difference, we can reduce the overall degree of irreversibility.
This is illustrated in the figure using N large energy reservoirs, each with a temperature slightly larger than the last. Because such reservoirs are so much larger than the envisaged system (denoted by SYS), we can treat the reservoir temperatures as constant. As the system is successively put into thermal contact with reservoir 1, then 2, then 3, … its temperature rises from one temperature to another. For example, suppose N = 1001, T1 = 20 °C and each successive temperature is 0.01 °C higher than the previous one. Then after the 1000 step process, the system's temperature will have increased by 30 °C.
If the number of steps is instead 1 million and the single-step temperature increase is always 0.00001 °C the same final temperature is reached, but in an even more nearly reversible way. That is, when the 1 million steps are followed in the reverse order, the individual equilibrium states, step by step, will be the same—but there exists a continuum of equilibrium states and temperatures between successive reservoir temperatures. We would have to increase the number of reservoirs without bound and decrease the successive temperature differences toward zero to achieve, as a limiting case, true reversibility.
For both conceptual and mathematical purposes, it is helpful to envisage the limit of infinitely many reservoirs and an infinite number of individual steps to accomplish the process in a reversible way. In this limit, if we took the system back over the energy reservoirs in reverse order, both the system and also each reservoir would return to its initial thermodynamic state, passing through the same equilibrium states during heating and cooling. Obviously, because this would take infinite time, it can only be useful as a conceptual and mathematical tool. We cannot achieve reversibility in a laboratory.
Mass Exchange
Given that the three primary ways to alter a system's energy is by a work, heat, or mass transfer process, it is natural to complete the discussion here with the latter case. A familiar process to us is a leaky automobile or bicycle tire, where air from within a tire leaks to the atmosphere. This process is an irreversible one—namely, it is not possible to put the air back into the tire without altering the surroundings. For example, we could put a tire patch on and use an air pump to blow the tire back up. However, in doing so, we would be transferring our own energy, which was derived from chemical reactions of oxygen with the food we eat. The food has changed form and our bodies are kept at about 37 °C during the process. Furthermore, the pump warms up as the air is pumped and heats the surroundings. Clearly, a number of things about the surroundings change in order to put air back into the tire.
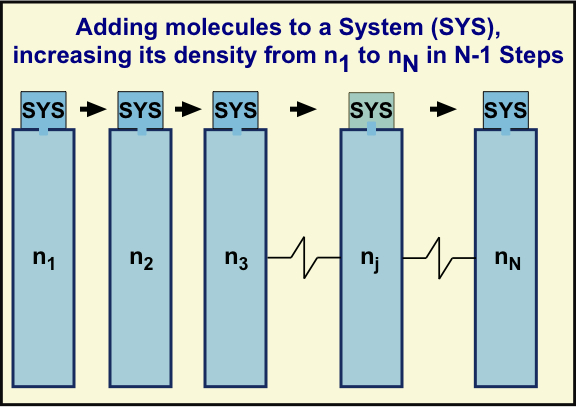
In the limit of infinitely many reservoirs and individual steps, with the successive changes in number density approaching zero, we can envisage a reversible process. If we took the system back over the reservoirs in reverse order, both the system and also each reservoir would return to its initial thermodynamic state. Most important, every intermediate state would be reached during the number density increases and decreases. The same exact path would be followed both ways, and no other changes in the universe would occur. This characterizes reversibility.

An old-fashioned incandescent light bulb operates by passing electric current through a narrow metal filament. The filament temperature is typically about 2400-2700 °C. The energy transfer through the large temperature difference is definitely irreversible. There is no way to bring the energy released primarily by electromagnetic radiation—i.e., heat and light—back to the filament without modifying parts of the universe outside the light bulb.
Any object whose temperature is higher than the surroundings will radiate energy to those surroundings. For example, humans "glow" when they are warmer than their surroundings, a fact that is made clear by infrared photographs.

What is not evident in the photographs is that the surroundings also radiate primarily in the infrared. The radiation of infrared frequencies from the hot cup is stronger—i.e., has a higher power level—than the radiation energy the cup receives from the lower-temperature man and surrounding air. Therefore, it cools over time. In contrast, the cold glass receives more infrared energy than it emitts, and its temperature increases over time.
Returning to the light bulb, when we turn it off, it cools to the temperature of the surroundings and becomes invisible to an infrared camera. As it cools it heats its surroundings ever more slowly (lower power level), and the heating process approaches a reversible one.
The main point is that all lamps radiate irreversibly when they emit visible light. Incandescent lamps run at higher temperature than fluorescent lamps and heat much more than they light. The energy they emit in the visible part of the electromagnetic spectrum is much less than that emitted in the infrared. Fluorescent lamps emit a higher fraction of energy of visible frequencies , and LED lamps emit an even higher fraction of light. We can think of incandescent lamps as operating "more irreversibly" than fluorescent lamps, and much more irreversibly than LED lamps.
After they have been OFF for a while, all lamps heat their environment at the same rate as they are heated by the environment. This can be viewed as a steady state situation. If on the other hand, radiative processes are simply ignored given their invisibility on a macroscopic scale, this can be, and usually is, viewed as a condition of thermodynamic equilibrium. Neither the thermodynamic state of the lamp or surroundings is changing perceptibly. However, realizing that radiation is emitted and received by lamp and surroundings, it is clear that this is a dynamic equilibrium.
For small temperature differences between lamp and environment, there is a nearly reversible energy flow. Only in the full limit of zero temperature difference can a heating or cooling process be viewed as reversible. In the full reversible limit, nothing happens over finite time periods; i.e., it would take infinite time to generate a finite change in a system's thermodynamic state. This is a fact of life, often unstated, in thermodynamics.
Last updated: Wednesday, 24 April 2024 17:22:29