INTRODUCTION
I taught thermodynamics for the first time in 1963 and subsequently taught both "thermo" and also statistical mechanics many times. These subjects fascinated me, with the most fascination centered around entropy, its properties, and conceptual meaning. Many have written about entropy, but the topic is by no means a settled one. One aspect of entropy that has not received much attention is that it is a measurable property for any system in "thermodynamic equilibrium"—i.e., a system's entropy has a definite numerical value when its temperature, pressure, volume, and the like are unchanging and there is no energy or matter flowing through it. Many discussions of entropy do not recognize that entropy is a numerical entity.
Furthermore, the entropy of any object, element, or compound approaches zero as the lowest possible temperature, absolute zero, is approached. As heating occurs and the temperature rises, so does the entropy. At any subsequent temperature, the corresponding entropy depends upon how much energy was added to the material, and how much of that energy is stored within it. This illustrates a close connection between energy and entropy.
Unfortunately, entropy discussions are often divorced from reality, ignoring both the numerical entropy and the close linkage between energy and entropy.
A major difficulty is that both thermodynamics and entropy can be approached in several rather different ways, making it difficult to grasp its essence. Perhaps because of this, many have oversimplified entropy as being a measure of disorder. This is problematic because the noun disorder is defined in the Oxford English Dictionary as: Absence or undoing of order or regular arrangement; confusion; confused state or condition.
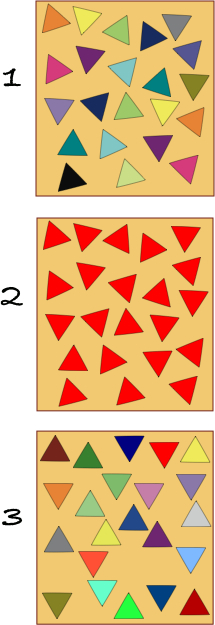
Most commonly, we tend to associate disorder with the irregularity of spatial arrangements, which we humans can sometimes recognize. But spatial order can be a tricky thing to discern. For example, Fig. 1 shows a group of 22 triangles that have differing, seemingly unpredictable angular orientations and colors. Figure 2 shows 22 triangles which all have the same color but still has differing angular orientations. In contrast, the 22 triangles in Fig. 3, which are randomized by color, each have one vertex pointing either up or down, which suggests a degree of order.
Do you find one of the figures more "ordered" than the other? My own perception is that Fig. 3 looks most ordered. However, it is difficult to say whether the color randomness in Fig. 3 actually gives more or less "disorder" than the orientational randomness of Fig. 2. Different people could reasonably come to differing conclusions. This points to a major problem with the disorder concept: It is subjective. Further, thermodynamics entails energy, and simple images such as Figs. 1, 2, and 3 cannot address the role of energy at all.
An illustrative example is the heating of ice and the subsequent liquid water. Consider the melting of one kilogram (kg) of ice. The resulting water is sometimes viewed as being more disordered than the crystalline ice, for which molecules are arranged regularly. That regularity exists to a lesser degree in the liquid, which takes on the shape of its container or simply spreads out into a thin surface layer. And when the liquid water is heated and vaporized, the water vapor is seen as more disordered than the liquid—i.e., the vapor becomes less ordered spatially. Each molecule expands through whatever volume is available, unlike in the liquid, whose volume does not change significantly as it is heated. The molecules in the liquid are kept more organized.
It is known that the numerical entropy per kg of water vapor exceeds that of liquid water, which exceeds that of ice. Therefore, the disorder metaphor gives the misleading impression of being a valid metaphor. However some strong caveats are needed. Read on.
It turns out that the situation is far too subtle for the one-word descriptor disorder to possibly suffice. For example, if 1 kg (kilogram) of water vapor is expanded to twice its volume at a constant temperature, it is known that its entropy increases. But has the vapor really become more disordered? Its molecules are farther apart but what definition of disorder would lead to the conclusion that disorder increases with increasing volume?
Further, 2 kg of ice has twice the numerical entropy of 1 kg of ice at the same temperature. Given that its molecules are just as regularly arranged as for the 1 kg sample, in what sense is it more disordered? What definition of disorder supports this and the expansion of a gas?
Indeed if expansion is believed to generate disorder, how do we explain the fact that as water is heated from 0 °C to 4 °C its volume decreases, while its numerical entropy increases? If the process is done in reverse, cooling the water, there is expansion, with a corresponding entropy decrease! This is counter to the notion that expansion leads to higher entropy.
Evidently, as I mentioned earlier, a judgment on whether disorder increases, decreases, or remains unchanged seems to be arbitrary and subjective. The unfortunate metaphor linking entropy and disorder is typically applied inconsistently, ignoring existing counterexamples. The bottom line is that disorder is a very poor metaphor for understanding entropy. We can, and will, do better trying to interpret the meaning of entropy.

As indicated above, intimately related to entropy is energy, a quantity that is difficult to define sharply. Commonly, students in beginning physics learn about kinetic energy, the energy of motion. The faster an object moves, the more kinetic energy it has. They learn too about potential energy, usually starting with gravitational potential energy (GPE). A bird has more GPE when it's in the air than when it is on the ground. To be precise, the GPE is a mutual energy of the bird–earth system. This energy comes from the attractive force pulling the bird toward earth (and earth toward the bird!). A gas of many molecules, each of which moves continually, has a total energy that comes from the kinetic energies of the molecules and the mutual potential energies related to the intermolecular forces between pairs of molecules. In thermodynamics, this energy which is stored by the gas is called internal energy.
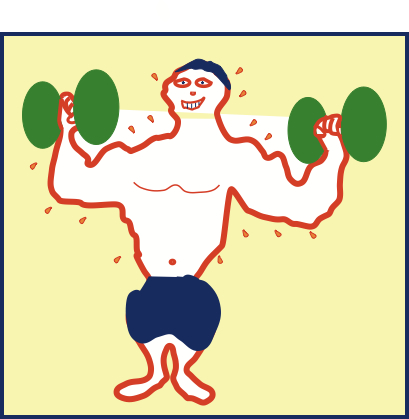
• Physical work, namely, one or more applied forces pushing or pulling the system, typically deforming it. Some examples are hitting the system with a hammer, sawing it into pieces, grinding its surface, and putting a heavy weight on top of it, deforming it (even if slightly).
• Heating (or cooling), namely putting the system in thermal contact with something that is hotter or colder than the system. It is not necessary for the two objects to touch. This is clear from the heating of earth by the sun, which is millions of kilometers away.
• Mass transport, which is the transferral of mass into or out of the system. An example is when the thermodynamic system is an automobile and the transfer is filling the gasoline tank.
All three are illustrated in the bodybuilder cartoon. Physical work is done on the dumbbells as they are being lifted, and the heart does work pumping blood through the body to oxygenate cells. The body is typically warmer than the air and if so, the body heats the surroundings; i.e., it transfers energy to the air. Finally, the bodybuilder breathes in and out exchanging material (e.g., oxygen and carbon dioxide) with the air. Furthermore, to maintain normal body temperature, the bodybuilder transfers water and/or water vapor to the surroundings—as the figure illustrates.
In each case, the above actions typically alter a system's internal energy and its entropy. Indeed all the thermodynamic processes of which I am aware entail a spatial redistribution of energy and a concomitant change in the system's entropy. The redistribution can be a subtle one. For example, the so–called free expansion of a gas into a space that was initially empty of matter entails neither physical work, nor a heat process, nor mass transport into or out of the gas. But this is a thermodynamic process, characterized by a spatial redistribution of the system's molecules and their energy into a larger volume, and a corresponding increase of the system's entropy. I'll expound on the spatial energy concept in later essays.
The Historical Origin of Entropy

This definition did not come out of the blue, but rather from a detailed mathematical examination of thermodynamic cyclic process. These are processes that begin and end in the same thermodynamic state. I'll discuss these in more detail in a future essay, but for the moment, I'll focus only on Clausius' results. He used the symbol S for entropy and that is still the commonly used entropy symbol today. He expressed a small entropy change dS as
dS = dQ/T,
where dQ is the small energy transfer that induces the the corresponding entropy change dS (the symbol "d" commonly connotes a very small change). T is the Kelvin absolute temperature, which equals the temperature on the Celsius scale plus 273.15 (often this is approximated by 273). For example, a room temperature of 22 °C (about 72 °F) is 295 K. The Clausius entropy form implies that entropy has the units joules/K, i.e. energy per unit temperature. Again, this points to the entropy-energy connection.
By convention, the degree symbol ° is not used on the Kelvin scale. Perhaps the most notable characteristic of the Kelvin scale is that its zero point (0 K) represents the lower limit of how cold anything can be. In fact, it is believed that 0 K cannot actually be reached, but can be approached arbitrarily closely. The achievement of such low temperatures requires specialized cryogenic laboratory equipment. The lowest temperature ever achieved in a cryogenic laboratory is about 0.0000000001 K = 1 x 10-10 K.
The main point here is that Clausius defined entropy change in terms of an energy transfer. Thus, entropy is linked to energy through its original definition by its creator, Clausius. Unfortunately, the value of this in understanding entropy qualitatively is not appreciated in many of the common textbook treatments of thermodynamics. It is especially absent in the inadequate and misleading statement, "entropy is a measure of disorder."
Statisical Mechanics

In principle, statistical mechanics enables the calculation of thermodynamic quantities from the masses of molecules and mutual potential energy between pairs of molecules. Most notably, Boltzmann made an ingenious discovery. He found a way to define entropy, and although it is very different looking from the definition by Clausius, is entirely consistent with that definition.
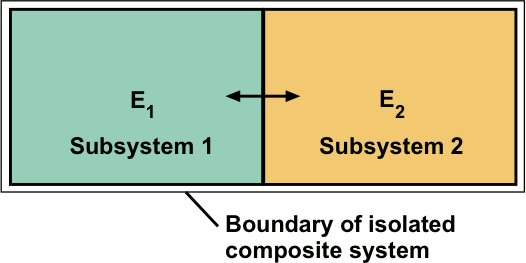
E1 + E2 = E = constant.
Each subsystem energy is variable and nature selects a particular average energy for each subsystem when the two subsystems reach thermodynamic equilibrium with one another. Boltzmann's goal was to explain what governs the equilibrium values of E1 and E2.
He understood well that it is impossible to describe the positions and velocities of the enormous number of molecules in a typical gas. Instead, his plan was to describe statistical properties. He defined a probability W, that the subsystems had specific energies E1 and E2. He chose the letter W to represent Wahrscheinlichkeit, the German word for probability. Given that subsystems 1 and 2 behave largely independently of one another when equilibrium prevails, the probability of finding energies E1 and E2 has the form W = W1 x W2. This takes advantage of the property that probabilities for independent events multiply. Seeking an additive function of the two subsystem energies, he defined the entropy function as
S = k log W = k log W1 + k log W2
Here, log W is the logarithm of the probability W. Boltzmann took advantage of the well known property that the logarithm of a product W1W2 is the sum of the logarithm of W1 and W2. The factor k is the so-called Boltzmann constant, k = 1.38 x 10-23 joules/K (this matches the units of the Clausius entropy change dS = dQ/T, with the energy dQ in joules and temperature T in kelvins).
The resulting equation expresses the entropy of the isolated system as the sum of entropies of the two interacting subsystems,
S = S1 + S2
Boltzmann's association of entropy with probability has been somewhat lost over the years, and many authors seem to be unaware of it and, in particular, to Boltzmann's focus on interacting subsystems of an isolated system. This point has come to light in recent years through the excellent journal publications and textbook on thermodynamics and statistical mechanics by Robert Swendsen of Carnegie Mellon University.
It is sensible to examine interacting subsystems because no actual system is entirely isolated from its environment. For example, even the most well-insulated cryogenic containers, which are designed to keep liquid helium at ultra-low temperatures within several degrees of absolute zero are not perfect insulators. They merely slow down the energy flows through the container walls. For our example, system 1 might be a chosen system of interest and system 2 might be its surroundings.
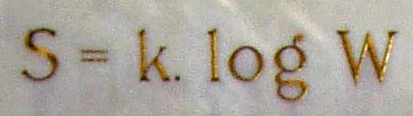
Boltzmann did not use the factor k. Rather, that constant was introduced and first evaluated numerically by Max Planck. Despite Planck's important involvement, k is traditionally called Boltzmann's constant. At least in part, this is likely because Planck has another fundamental constant named after him! Planck's constant is an important constant that arises in quantum theory.
The details of all this are not the focus here, but I wish to emphasize an essential point: Boltzmann's entropy equation is meaningful only with the specification of a total system energy and the probabilities of finding specific energies of the interacting subsystems. Thus, it is eminently clear that entropy is linked with energy in its definitions of thermodynamic entropy by both Clausius and Boltzmann.
For example, there might be two non-overlapping spatial regions in a gas with two different densities. Boltzmann calls this "molar–order." If the regions have the same density, this is "molar–disorder." The word "molar" suggests a macroscopic region. Within one of these regions there might be a small group of molecules displaying regularity, say, moving toward its nearest neighbor. Boltzmann referred to such situations as "molecular–order"—and when no such regularity exists, there is "molecular–disorder." Of paramount importance is Boltzmann's assumption, that at a given instant of time, "the motion is molar– and molecular–disordered, and also remains so during all subsequent time." Boltzmann was expressing his believe that molecules and their energies tend to become as uniformly distributed as possible. This is consistent with the view that energy spreads throughout a system to the extent possible, which helps me understand real thermodynamic processes.
Boltzmann applied his ideas to gases, and one might wonder if they apply in some sense to solids and liquids. The answer is yes, with the key ingredient being that for an initially molar–ordered system, if it is not constrained, it will evolve to a molar-disordered one, as defined by Boltzmann. The key ingredient in this is that the evolution entails a redistribution of energy. Such "energy spreading" will be discussed in my essay "Irreversibility and Energy Spreading," and will recur throughout many of the essays.

A special case in Gibbs' framework is when the energy is known exactly—or within a narrow energy range—in which case, the Gibbs entropy expression reduces to Boltzmann's. Of primary interest here, as before, is that energy plays a fundamental role in Gibbs' development. In particular, energy and entropy are intimately related to one another.

A fourth development of thermodynamic entropy came out of Claude Shannon's mathematics-centered information theory. That theory was aimed at understanding the coding of messages during the second world war. In 1957, Edwin T. Jaynes published an article entitled, "Information theory and statistical mechanics." In his abstract, he wrote,
"Information theory provides a constructive criterion for setting up probability distributions on the basis of partial knowledge,and leads to a type of statistical inference which is called the maximum-entropy estimate. It is the least biased estimate possible on the given information; i.e., it is maximally noncommittal with regard to missing information. If one considers statistical mechanics as a form of statistical inference rather than as a physical theory, it is found that … in the resulting 'subjective statistical mechanics,' the usual rules are thus justified …"
What this means is that for macroscopic systems, where there are too many molecules to keep track of individually, we can use probabilities to find the most likely system energy when it is in thermal contact with its constant-temperature surroundings. For dilute gases, for which molecules behave relatively independently of one another, we can find the most likely way energy is distributed among individual molecules. Information theory enables us to find the least–biased set of probabilities. When Jaynes specified, in accord with statistical mechanics itself, that the average energy of the system was a known quantity, he found a one-to-one connection between mathematical objects related to information theory and the physical quantities of statistical mechanics and thermodynamics.
In the process he related Shannon's missing information function to the thermodynamic entropy, and also was led naturally to make a correspondence between a purely mathematical object that arose when looking for the least–biased probabilities and the physical temperature. The Shannon missing entropy has the same mathematical form as that found by Gibbs. Also, if the energy is assumed to be known exactly, the Boltzmann entropy expression that appears on Boltzmann's tombstone emerges once again. Notably, as with the Clausius and Boltzmann developments, a strong connection between energy and entropy emerges.
A very important insight that emerges from Jaynes' work is that thermodynamic entropy can be interpreted as a measure of missing information, or equivalently, uncertainty. This is an interpretation that has a solid basis in mathematics, unlike the poor, but too commonly used disorder metaphor. Returning to the above example of water vapor expanding to twice its original volume, the corresponding entropy increase can be interpreted as representing an increase in the uncertainty of the molecular positions. That is, because each molecule has more volume on average in which to roam, its position at any time is more uncertain than when the vapor was in a smaller volume.
Concluding Remarks
I have illustrated how an intimate connection of energy with entropy clearly surfaces in all four developments of thermodynamics and entropy. In the remaining essays, I hope to present a cogent view of energy, entropy, and the connections between them.
© 2013 Harvey S. Leff — Last updated: Friday, 26. April 2024 08:55 PM