CYCLES AND CLAUSIUS
Some Needed Fundamentals of Thermodynamics
Real-life thermodynamic processes can be messy to describe fully. When an object is heated, the heating is often not uniform—i.e, there are spatial regions of higher and lower temperature, at least temporarily. At times, temperature might fluctuate spatially so much that it is impossible to even specify a temperature for the system until things settle down to equilibrium. Similar difficulties occur for cooling processes and also for the behavior of matter under pressure and volume changes. For these reasons, physicists have focused on equilibrium properties and near-equilibrium processes.
CTRs and RWSs. To aid in this, they have invented mental constructs that enable slow, controllable heating, cooling, and work processes. The first construct is a constant-temperature reservoir (CTR). This is a massive entity that is always in thermodynamic equilibrium. It can exchange energy by heat processes without its temperature changing perceptibly. It is assumed to remain homogeneous even when energy exchanges are rapid. That is, its response time is nearly zero. I already have used such reservoirs, which I referred to as energy reservoirs in the essay Power and Reversibility. Obviously, a CTR is an idealization that is used to enable us to focus on changes in a chosen system of interest.
Real-life thermodynamic processes can be messy to describe fully. When an object is heated, the heating is often not uniform—i.e, there are spatial regions of higher and lower temperature, at least temporarily. At times, temperature might fluctuate spatially so much that it is impossible to even specify a temperature for the system until things settle down to equilibrium. Similar difficulties occur for cooling processes and also for the behavior of matter under pressure and volume changes. For these reasons, physicists have focused on equilibrium properties and near-equilibrium processes.
CTRs and RWSs. To aid in this, they have invented mental constructs that enable slow, controllable heating, cooling, and work processes. The first construct is a constant-temperature reservoir (CTR). This is a massive entity that is always in thermodynamic equilibrium. It can exchange energy by heat processes without its temperature changing perceptibly. It is assumed to remain homogeneous even when energy exchanges are rapid. That is, its response time is nearly zero. I already have used such reservoirs, which I referred to as energy reservoirs in the essay Power and Reversibility. Obviously, a CTR is an idealization that is used to enable us to focus on changes in a chosen system of interest.
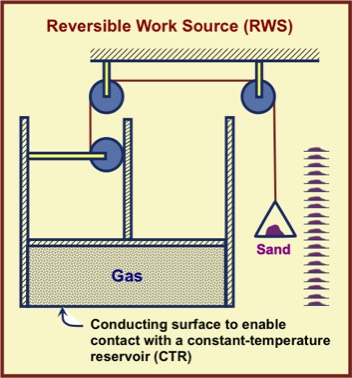
Assume the "floating" is both frictionless (another idealization) and sufficient to contain the gas without leaks. The assumption that sand can be moved with negligible energy input means that this movement can be done with arbitrarily small (and therefore imperceptible) energy. The basis of this assumption is that (a) horizontal motion with zero friction can be initiated and ended with zero work and (b) human ingenuity can reduce friction to very low values.
Note that in the figure, we can envisage the gas being put in thermal contact with a CTR, with a heat process through the bottom of the chamber containing gas. With such an apparatus, it is possible to take a gas from an initial thermodynamic state to another along a variety of different paths, depending on how much mass is added to or subtracted from the pan as the gas is moved from one CTR to another. In particular, it is possible to take the gas through a cyclic process.
If the gas is taken through a complete cycle—namely, ending in the same thermodynamic state in which it began—there will be no net thermodynamic change in the gas. However, there will generally be changes in one or more CTRs and also changes in the mass distribution of sand on the column of shelves.
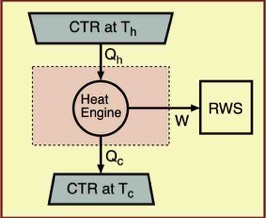
It is well known that the second law of thermodynamics limits the efficiency of heat engines. Learning this is a major result of the success of thermodynamics. Heat engines are devices that consist of a working fluid such as a gas, and in our idealized models, have variable linkages to external energy reservoirs and work sources (CTRs and RWSs). Real heat engines such as automobile internal combustion engines differ in that their working fluids are burned and must be replaced.
Designing real heat engines is a task undertaken by mechanical engineers. This is a complex issue because combustion and the resulting quick expansion and necessary exhaust of combustion products are non-equilibrium processes.
In contrast, the idealized models that are commonly studied by physicists operate cyclically using a non-expendable working fluid and traverse slow, typically reversible paths. During one cycle, the fluid exchanges energy with one or more CTRs, converts part of that energy to work on an external RWS, and rejects the remaining energy to one or more lower-temperature CTRs.
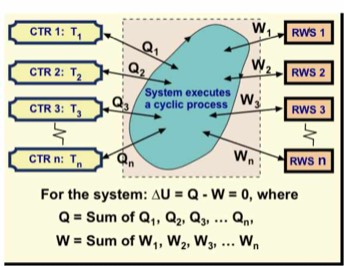
As alluded to already, an important characteristic of such a cyclic process is that after a complete cycle the only changes in the universe are those in the energy reservoirs that were involved and the work source and/or recipient. For a heat engine, these changes are typically in one or more constant-temperature reservoirs and the RWS on which work was done.
The figure shows a heat engine that transfers energy Qh from a CTR at temperature Th to the heat engine's working fluid, rejects energy from the working fluid to a CTR at temperature Tc , and in the process, does work W on a RWS. Because the heat engine's working fluid executes a cycle, it thermodynamic state has not changed. Thus in one cycle the net energy from CTRs used for heating is Q = Qh - Qc.
The first law of thermodynamics dictates that because ∆U = Q - W = 0 for the working fluid, then Q = W. I have assumed that the "heats" Qh and Qc are positive numbers and I account for energy loss from the working fluid by a minus sign. Because energy is conserved, Qh must exceed Qc or there would not be enough energy for the heat engine to perform work, which is its main function. The work done must be the difference, Qh - Qc.
Q1. Is a heat engine that converts all the energy from a high-temperature reservoir into work possible?
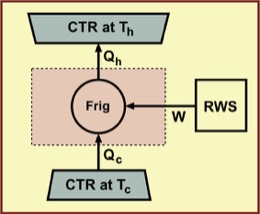
Q2. Is a refrigeration cycle possible that moves energy from a low-temperature reservoir to a higher-temperature reservoir without an external work source?
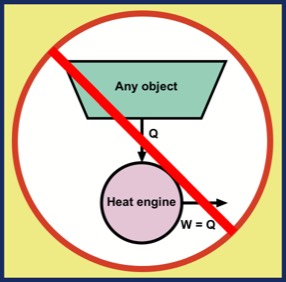
The answer to both questions is an unqualified NO. Question Q1 was ruled out by a law clarified by William Thomson in 1851: "It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects." Here, "mechanical effect" refers to what is now called work.
A more clear and modern statement comes from Max Planck in 1897: "It is impossible to construct an engine which will work in a complete cycle, and will produce no effect except the raising of a weight and the cooling of a heat-reservoir." All of this means that it is not possible to extract energy from an object, cooling it, and produce an equal amount work W = Q without some other effect in the universe. This statement of impossibility is illustrated in the figure.
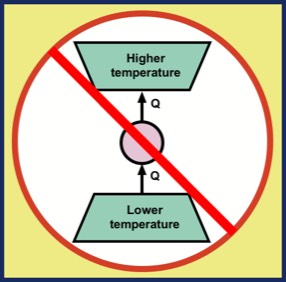
Despite the fact that these two statements of the second law of thermodynamics appear very different, it is easy to see that if one is violated, so is the other.
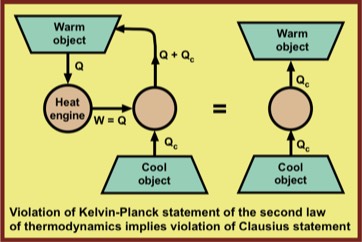
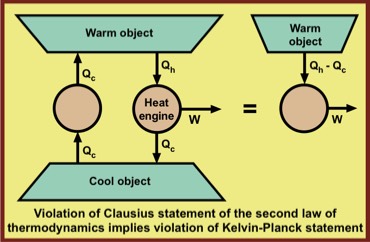
William Thomson's contribution

In an actual real-life, irreversible refrigerator, a fluid refrigerant is pushed through a loop, heating it. That is, the work of compression increases the fluid's internal energy and temperature. The fluid is then passed through a coiled heat exchanger (hot coil), where it can exchange energy with the room air. Because it is hotter than the room air, it sends energy to the cooler kitchen surroundings by a heat process. Note: There is no spontaneous energy transfer from lower to higher temperature!
After passing through the hot coil, the fluid is then expanded quickly using an "expansion valve," cooling the fluid considerably, much as the hair spray coming out of a pressurized spray can is cooled. The expansion makes the fluid cooler than its surroundings within the refrigerator. Next, the cold fluid is passed through another coiled heat exchanger (cold coil) where it absorbs energy from the the refrigerator compartment and food it contains. Note: Again there is no spontaneous energy transfer from lower to higher temperature!
The net result is that the work process that is powered by the motor causes the fluid to raise the temperature of the hot coil, and the subsequent rapid expansion leads to the low temperature of the cold coil. Energy does not flow spontaneously from lower to higher temperature at any point in the cycle, and no thermodynamic laws are violated.
Because there are energy transfers between finite temperature differences between each coil and its surroundings, the heat processes both within and outside the refrigerator are irreversible.
Thumbnail Sketch of Clausius' Thermodynamics Accomplishments
Rudolf Clausius (1822 - 1888) was a major contributor to the development of thermodynamics as we know it. His work followed that of Sadi Carnot, whose Reflections on the Motive Power of Fire made clear that there is a maximum efficiency for any heat engine operating between higher and lower temperature energy reservoirs, and this efficiency depends only on those two temperatures and not any details of the heat engine. Unfortunately, Carnot's work was done within the framework of the caloric theory, before the concept of energy in thermodynamics was fully understood.
Clausius approached the subject differently and his work, along with the contributions of James Joule, William Thomson (aka Lord Kelvin), led to our present understanding of the role of energy in thermodynamics. One of the most important ideas to emanate from the work of Clausius are these:
(1) thermodynamic systems store energy U called internal energy;
(2) the internal energy is a function of the thermodynamic state and does not depend on how that state was achieved;
(3) there are two laws of thermodynamics;
(4) the first law of thermodynamics assures that the principle of energy conservation is satisfied for thermodynamic processes;
(5) the second law of thermodynamics recognizes that not all processes that conserve energy actually occur In nature;
(6) the second law of thermodynamics can be framed in terms of a new thermodynamic function of state called entropy;
(7) "The energy of the universe is constant; the entropy of the universe tends toward a maximum."
Notably, Clausius was led to the entropy function through the clever use of cycles. His arguments are outlined in my article, ‘‘Reversible and irreversible heat engine and refrigerator cycles,’’ Am. J. Phys. 86, 344-353 (2018), which can be viewed HERE.
To navigate to Publications, click HERE.
Rudolf Clausius (1822 - 1888) was a major contributor to the development of thermodynamics as we know it. His work followed that of Sadi Carnot, whose Reflections on the Motive Power of Fire made clear that there is a maximum efficiency for any heat engine operating between higher and lower temperature energy reservoirs, and this efficiency depends only on those two temperatures and not any details of the heat engine. Unfortunately, Carnot's work was done within the framework of the caloric theory, before the concept of energy in thermodynamics was fully understood.
Clausius approached the subject differently and his work, along with the contributions of James Joule, William Thomson (aka Lord Kelvin), led to our present understanding of the role of energy in thermodynamics. One of the most important ideas to emanate from the work of Clausius are these:
(1) thermodynamic systems store energy U called internal energy;
(2) the internal energy is a function of the thermodynamic state and does not depend on how that state was achieved;
(3) there are two laws of thermodynamics;
(4) the first law of thermodynamics assures that the principle of energy conservation is satisfied for thermodynamic processes;
(5) the second law of thermodynamics recognizes that not all processes that conserve energy actually occur In nature;
(6) the second law of thermodynamics can be framed in terms of a new thermodynamic function of state called entropy;
(7) "The energy of the universe is constant; the entropy of the universe tends toward a maximum."
Notably, Clausius was led to the entropy function through the clever use of cycles. His arguments are outlined in my article, ‘‘Reversible and irreversible heat engine and refrigerator cycles,’’ Am. J. Phys. 86, 344-353 (2018), which can be viewed HERE.
To navigate to Publications, click HERE.