Spreading is a phenomenon that is very familiar to us. It is detectable by humans when they smell good or bad things in the air, see brownish smog, and find oil and other pollutants in water. Spreading occurs invisibly when we heat water, sand wood, mix sugar in coffee, and the like. Spreading is a natural irreversible phenomenon. That is, the spreading occurs naturally, but UN-spreading does not. Oil droplets dispersed in an ocean do not coalesce and return to the leaking tanker that emitted them. Understanding spreading can help understand the concept of thermodynamic irreversibility.
• Diffusion: Spreading of particles and energy
If we leave a perfume bottle open for a while, the smell of perfume will permeate the room. Volatile perfume molecules leave the bottle and move randomly through the room. When the concentration of perfume molecules becomes sufficiently large near your nose, your olfactory system sends a message to your brain that you smell perfume.
Such diffusion is an excellent example of spreading phenomena. Highly mobile molecules get bounced around by other molecules and tend to move in all directions. Gaseous perfume molecules can bounce off the bottle's side walls, remaining in the bottle. But molecules that move upward have an easy path out of the bottle. And once they are out, they are free to move in any direction, bumping into molecules of air as they travel. The release of more and more perfume molecules into the air can continue for quite a while because the number of perfume molecules is enormous, and a typical room is much larger than a perfume bottle. Given enough time nearly all the original perfume molecules will be out of the bottle.
You would find it inconceivable that once out of the bottle, the perfume molecules could reverse their paths and work their way back into the bottle again. The fact that you cannot fathom such an occurrence is strong testimony that the spreading process is a natural irreversible phenomenon. A similar phenomenon occurs with the baking of bread, in which case the delicious scent of bread can be detected throughout a home, possibly quite far from the kitchen. Furthermore, we are all familiar with the spreading through air of unpleasant odors. Enough said about that.
When gas molecules diffuse through air, they carry with them the energy they store. Thus:
diffusion is an irreversible process that spreads not only particles, but also their energies, spatially.
The mental picture of molecules spreading their masses and energies throughout a volume does not explain irreversibility, but provides a way focus on its essence in a familiar way.
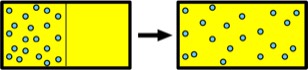
In the process, zero work is done on the gas, which simply diffuses naturally from a region of higher to lower density region. The work is zero because although the walls exert forces on the gas, those forces do not act through a nonzero displacement.
Why does the gas diffuse this way? Initially, in the left chamber, molecules move in all directions and it is just as likely for a molecule to leave a small interior region as it is for another molecule to arrive there. So on average, the number of particles in the region does not change. However, just after the partition breaks, the region to the right has few molecules and it is more likely for molecules to arrive in the right half than to leave that region. This situation persists until the density in the left half equals that in the right half, illustrating the essence of diffusion.
Because the expansion is into an empty chamber, and requires zero work, this phenomenon is called a free expansion. Such expansions were performed experimentally by a number of researchers, including a notable one by thermodynamics founder, James Joule. He observed in 1845 that for dilute gases like air, the gas temperature after the expansion was no different from that before the expansion.
When the central partition breaks, there is a net rightward force on the gas because the force of the left wall is no longer balanced by the leftward force of the central partition. The laws of mechanics tell us that the center of mass of the gas must accelerate rightward until the gas reaches the right wall and comes to equilibrium. This rightward acceleration occurs as the gas diffuses. When mechanical equilibrium is reached, the left and right walls exert forces of the same magnitude, and the net force on the gas is again zero.
As in the case of perfume diffusion: (1) the process is irreversible, and (2) energy as well as particles spread spatially through the container.
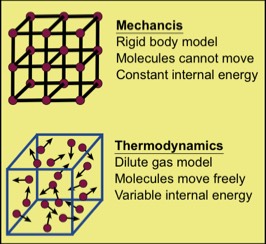
Classical mechanics deals with the motion of "point particles," idealized particles with zero volume, yet finite mass. Such imagined particles cannot store internal energy. Classical mechanics also deals with the motion and forces on idealized "rigid bodies," which consist of molecules imagined to be fixed in place, as if connected by completely rigid (yet massless!) bars. Because of this rigidity, the internal energy of a rigid body, if any, cannot be changed. Neither point particles nor rigid bodies exist, but are imagined. Neither is a thermodynamic system. Remember, thermodynamics is the science dealing with internal energy and its changes by work, heat and mass transport processes. Point particles and rigid bodies cannot exchange internal energy.
In contrast, real macroscopic systems consist of molecules that can gain and lose energy, and such objects can, and do, engage in thermodynamic processes. An example is a gas, depicted symbolically here. By moving one of the container walls toward or away from the gas molecules, one can do positive or negative work on the gas. This can be done in principle by replacing the wall by a movable piston that can slide frictionlessly.
Such a change in volume generally entails a redistribution of the internal energy of the gas; i.e., a spreading of energy. Additionally, by heating one of the walls, energy is transferred to the molecules of the wall, and subsequently to the gas molecules. This is a heat process which again, entails a spreading of energy. We can also puncture a wall to let some molecules out, which is a mass transport process. Obviously, that also involves a spatial spreading of energy. These envisaged thermodynamic processes show that gases are indeed thermodynamic systems.
Classical mechanics is relatively transparent in the sense that we can often see all the objects involved, measure the forces on them, and observe their bulk velocities and accelerations. However, thermodynamic processes occur, they are often invisible. An example is the conversion of macroscopic bulk energy to invisible internal energy within macroscopic matter. In such cases, the situation is less transparent, but often more interesting. Perhaps most important, spatial energy spreading in actual physical systems is always irreversible.
Early on in physics courses, students encounter collisions that are fully or partially inelastic. This means that some of the kinetic energy of one or more macroscopic objects is transformed to the invisible energy form of internal energy. This is evident for example in collisions between objects.

Next a solid rectangular frame with vertical rods is added to the cart. Taut rubber bands with brass disks attached are strung horizontally between the rods, as shown in the figure. This is a model of a solid, with the brass disks representing molecules and the rubber bands representing molecular bonds—i.e., the forces between the molecules. If one plucks the rubber bands, they and their brass disks oscillate visibly. This simulates "heating," though strictly, the jiggling results from a mechanical process.
To get to the heart of inelastic collisions, the cart with the added frame is rolled on the floor toward a wall, inducing a collision. Two new phenomena are observed. First, the cart either comes to a nearly complete stop or bounces back at a noticeably reduced speed. Second, the collision induces vibrations of the brass disks and rubber bands. This is illustrative of what happens in a partially inelastic collision, where the initial kinetic energy of one or more macroscopic objects is transformed to internal energy associated with individual molecular kinetic energies. The increased jiggling is similar to the "heating" by plucking the rubber bands. More correctly, the kinetic energy of the cart's motion has been transformed to kinetic energies of brass disks and rubber bands. Calling the effect "heating" uses an overly simplified, one-word description to shield what is really going on energetically.
Interestingly, the rubber bands' oscillations get fully damped out as their vibrational energies are absorbed by the rubber's molecules themselves, which makes them jiggle a bit more. The collision of the cart-rubber band-brass disk system with a wall simulates an inelastic collision visibly, while the latter damping of the rubber band and disk oscillations leads to an invisible microscopic phenomenon: bulk rubber band kinetic energy is transformed to invisible internal energy—a jiggling of the rubber's molecules themselves. This is an example of the irreversible spreading of energy over large numbers of molecules.
It is notable that the jiggling associated with thermal activity that reflects the rubber's temperature, does not damp out. That is, the thermal jiggling persists in accord with the fact that the macroscopic rubber bands remain roughly at room temperature.
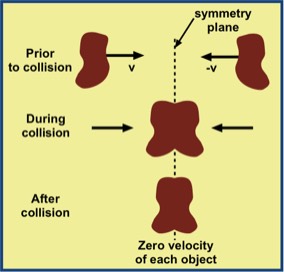
For a totally inelastic collision, for which all the original kinetic energy becomes internal energy, the total mechanical energy is obviously not conserved. This is clear because there is positive total kinetic energy before the collision and zero total kinetic energy afterwards. The (incomplete) reason sometimes given is that there is "heat generation." As with the cart-rubber band-disk example above, a more accurate statement is that the kinetic energy gets transformed into internal energy, with a concomitant temperature rise. Subsequently there is a heat process with the surroundings.
The collision is illustrated in the accompanying figure. The colliding objects are two identically shaped pieces of putty with equal masses, moving in opposite directions with the same speed. The fact that this is a mirror-symmetric collision assures that each piece of putty must behave in the same way. A consequence of this symmetry is that the points of contact between putty pieces all must lie in the plane of symmetry (dashed line). This implies that the force of each piece on the other acts through zero displacement—i.e., zero work is done on each piece by the other.
It is clear that the work-energy theorem of classical mechanics fails. It tell us that the external work done on a body equals the change in its translational kinetic energy. Failure is evident because there is a clear decrease in the kinetic energy of each piece, while the work on each putty piece is zero. How can a "theorem" be wrong? Simply, it can be wrong if it is applied outside its domain of validity.
That domain is pure mechanics, which applies only to point particles or "rigid bodies," whose internal energies cannot be changed. A piece of putty is not either of these. The work-energy theorem does not apply when mechanical energy of a macroscopic object is transformed into internal energy, which is what happens here.
The solution is to use a slightly modified form of the first law of thermodynamics, ∆U = W + Q from the essay on Energy Transfers. To remind you, ∆U is the change in internal energy U. The modification is simply to add the kinetic energy change ∆K to the left side, making that side of the equation the change in internal plus kinetic energy,
∆U + ∆K = W + Q generalized first law of thermodynamics
The two common energy transfers, work W and heat Q, are the same as they were in our original discussion. Note that in classical mechanics, where ∆U = Q = 0, the latter equation reduces to the work-energy theorem: W = ∆K. The beauty of the generalized first law of thermodynamics is that the left side accounts for the change in total energy, enabling us to account properly for the principle of energy conservation, with the understanding that more than kinetic energy is involved. That is, kinetic energy can be converted to internal energy.
Applied to the either piece of putty, the modified form of the first law of thermodynamics shows that the internal energy change of each putty piece is the negative of its kinetic energy change plus any energy exchange Q from a heat process. Because the kinetic energy changes are negative (each piece loses all its kinetic energy), the minus sign assures that the internal energy change is positive for each piece before any subsequent heat processes occur, which makes sense.
The transformation of purely mechanical (kinetic) energy into internal energy is an example of dissipation. An appropriate definition of dissipate is: to scatter in various directions; i.e, to disperse. Thus, for a thermodynamic system, dissipation can be viewed as the spreading of energy over an enormous number of molecules.
During the collision, the extra kinetic energies of each molecule from the pieces' bulk motion becomes extra kinetic energy of the internal jiggling. In this way, energy is "dissipated" into the energies of a gigantic number of molecules moving in many different directions.
Could the reverse process occur, whereby some kinetic energy of jiggling spontaneously becomes bulk motion of the pieces? No repeatable experiment has ever been reported with such a result. Indeed, if you reported seeing such an event, it is likely that few people would take you seriously because this is contrary to our everyday experience. In other words, while mechanical energy commonly spreads over the molecules of macroscopic objects, UN-spreading does not seem to occur at all.
With this mirror-symmetric inelastic collision, I have shown how mechanics morphs into thermodynamics. Generally, in inelastic collisions, some or all the initial kinetic energy is transformed to internal energy. The energy that is transformed in the collision spreads within the colliding objects, and is shared by their many molecules, which jiggle a bit more swiftly. Such problems are in the domain of thermodynamics.
The conversion of kinetic energy of macroscopic objects to internal energy exemplifies spatial energy spreading, a natural, irreversible process. Irreversibility is assured because UN-spreading of internal energy to macroscopic mechanical energy is not observed.

Suppose you heat an initially cool piece of metal with a powerful electric heater. It gets hot first nearest to the heater. If the heater is then turned off, the added energy spreads through the metal and the entire metal becomes warm, as depicted in the time sequenced (top to bottom) figure.
Similarly, if you remove the warm metal from the fire and place it in a pot of cool water, the metal cools and the water heats until both have the same temperature. This too can be viewed as a spreading and sharing of internal energy. These examples of spatial energy spreading are consistent with the previously-mentioned definition of thermodynamics as: the science concerned with internal energy changes of macroscopic matter by heat, work, and mass transport processes.
When two objects at different temperatures exchange energy, what determines the stopping point of this exchange? Using the development of Rudolf, the stopping point is when the combined entropy of the two objects reaches a maximum possible value. I will discuss this approach, which is somewhat abstract—especially before an explanation of entropy has occurred!
Another way to view this is that when one object has a higher temperature than another and the two are placed in thermal contact, the one with higher temperature has more than its fair share of energy. As energy flows from the hotter to the colder, this inequity is decreased. Thermodynamic equilibrium occurs when "energy equity" exists. If the two objects are identical in size, mass, and composition, differing only in their temperature initially, then equity exists when each stores the same internal energy. If the two objects are not identical, the situation is less "obvious." I shall explain the general case in a later essay on the Boltzmann formulation of entropy.
The main point at this juncture is that in a heat process, energy spreads from hotter to colder until the distribution of energy is equitable. It turns out that such equity exists when the temperatures are equal. As with the conversion of kinetic to internal energy, heat processes are generally irreversible. In terms of spatial spreading, the UN-spreading of energy from an equitable to an inequitable distribution does not occur.

Our understanding of heat processes has increased considerably over the years. In the eighteenth century, the discoverer of oxygen, Antoine Lavoisier, proposed that a flowing fluid called caloric (also sometimes called vis viva) was involved in heating and cooling processes. It was believed that there was a fixed amount of this mysterious fluid in the world, and that it flowed into a piece of metal during heating and from the metal during cooling.
Why would caloric fluid flow this way? Perhaps because a hot object is more dense with caloric than a cool one, and caloric tends to spread until the densities, and resulting temperatures, of all objects involved are equal. At that time, it seemed sensible that caloric tended to spread until it was distributed uniformly.
Despite the aesthetics of this mental picture, the caloric idea was found to be incorrect, because it is possible to heat an object simply by rubbing it, which is a work process, not a heat process. For example, we rub our hands together to warm them in winter. The more we rub, the more warming, so if caloric exists, it must NOT be a conserved quantity: we can create any amount of caloric simply by rubbing for a sufficiently long time.
This point was made abundantly clear in the experiments of Count Rumford in the late 1790s. He noted that cannon barrels heated up while their insides were being bored (i.e., drilled and ground out). The longer a cannon was bored, the greater the amount of heating. So if heat were actually caloric, it could be created in arbitrarily large quantities, by doing what in Newtonian mechanics is called work—the application of force through through a displacement.
In the nineteenth century, a number of researchers, including Julius Robert von Mayer, James Prescott Joule, and Ludvig Colding, studied the generation of heat by work processes. Until this period, from about 1840-1880, it had been believed that caloric (heat) was a conserved substance. It was measured in calories, while mechanical work was expressed in units of force times distance, newton-meters nowadays. All three researchers found numerical values that connected mechanical work units with heat units.
The most accurate and extensive experiments done to obtain this numerical connection was by Joule, whose apparatus is shown here. It consisted of a rotatable paddle wheel powered by strings attached via pulleys to falling weights (not shown). The work done stirring the water inside the insulated chamber became internal energy of the water. This increased the water's temperature measurably, enabling Joule to calculate the internal energy increase of water for a known amount of work. Before Joule, the concept of internal energy did not exist.
Joule's experiment illustrates the transformation of mechanical energy, rotational kinetic energy of the paddle wheel, to internal energy of the water. As above, this entails spatial energy spreading that is irreversible. It would be more than remarkable if the internal energy spontaneously decreased, turning the paddle wheel in the reverse direction, lifting the weights that had lowered previously. As before, such UN-spreading does not occur in nature.
The common unit of work, the newton-meter, has come to be called a joule in honor of Joule's achievement. Today the joule is the energy unit adopted in the System of International Units, not only for work, but in fact for all energy types. The connection between the joule and calorie that is now used worldwide is
1 calorie = 4.186 joules
A caveat is in order. The latter calorie is NOT a food calorie. The food calorie is actually defined as one thousand calories, namely, one kilocalorie, commonly labeled Calorie (note upper case C). The connection with the joule is 1 Calorie = 4,186 joules.
To give an idea of the size of a Calorie, if one were lifting 1 kilogram (about 2.2 lb) books from floor level to a shelf 1 meter above the floor, the lifting of about 427 books would require a total work of 4186 joules = 1 Calorie. Actually, because the human body is roughly 10% efficiency, only about 42 books would need to be lifted for a human body to "burn" one food calorie. In order to lose one pound, the body must burn about 3500 Calories, which requires lifting nearly 150,000 1 kilogram books to a 1 meter height.
The difficulty of losing one pound solely by exercise is illustrated further by this statistic, which I found via an internet search. For a 150 lb person to burn 1 lb of fat, he/she would have to walk up over 23,000 stairs. At one stair per second, the task would take over six hours. This is why people go on weight-reducing diets rather than to try to lose weight by exercise alone!
Obtaining the connection between work and heat, the so-called mechanical equivalent of heat, was much more than simply finding a number that connects two units. The results of Joule, Mayer, Colding, and others was instrumental in showing that there exists a universal quantity called energy that can neither be created nor destroyed. It can change from one form to another—e.g., potential to kinetic, work to internal, kinetic to internal, and the like—but its total value does not change.
This understanding propelled the conservation of energy into prominence as one of the most fundamental principles of physics. In fact, a common definition of physics is “the branch of science concerned with the nature and properties of matter and energy.”
After it became clear that work-to-heat processes were consistent with the conservation of energy, the need to understand their irreversible nature led to the second law of thermodynamics. One way to view this law is that it is impossible to retrieve all the internal energy added by a natural energy spreading process. For example, imagine rubbing your hands together to warm them, and then having that resulting internal energy converted back, spontaneously moving your hands, without any muscular effort on your part! Of course, this would be science fiction. Such UN-spreading of internal energy simply does not occur.
Appreciation of the mental model of energy spreading, but not UN-spreading, within matter, among something like 1020 or more molecules provides a basis for understanding irreversibility. This can provide a sense of why real-life thermodynamic processes are irreversible, without a formal study of the second law of thermodynamics. Stay tuned for a future essay on the second law of thermodynamics and its relationship to energy and entropy.

The universe contains billions of galaxies, each with billions of stars. Each of these stars radiates electromagnetic radiation in all directions of space. This radiation spreads through all parts of space. In addition, cosmic microwave background radiation (CMBR), remnant energy that originated about 280,000 years after the big-bang origin of the universe, is likely between your eyes and this page. This CMBR impinges earth, and all other parts of the universe, from all directions. This is a great example of the phenomenon of spatial energy spreading and irreversibility.
Hundred of billions of stars in the universe are undergoing irreversible nuclear fusion, releasing gigantic amounts of energy that spreads spatially. Galaxies collide, inducing more energy spreading. Supernova explosions regularly spread large amounts of energy spatially. The phenomenon of energy spreading within stars, nebulae, and the like, is ubiquitous and is the way of the universe. The concept of spatial energy spreading is a powerful tool for interpreting and appreciating the irreversibility of nature.
To navigate to Power & Reversibility click HERE.