
• Energy is ubiquitous
It enables plants and animals to live and grow. It is released when the foods we eat engage in chemical reactions with the oxygen we breathe in. An energy type called internal energy is stored in metals, air, water, and in fact just about everything.
As our universe expands, even seemingly "empty" space contains "dark" energy. Outside Earth, energy literally drives the birth, lives, and deaths of stars, which are vessels that store and convert enormous amounts of energy into light, heat, and other energy forms. Indeed energy transformations run the Universe.
Humans’ digestive systems transform energy derived from their food, together with the oxygen they breathe, enabling their hearts to pump blood, their muscles to work, and their lungs to take in oxygenated air and expel carbon dioxide. Each step entails energy transfers.
Energy is delivered to our homes via electricity. The fossil fuels, natural gas, oil and coal—when mixed with oxygen from the air—release energy that humans use for heating buildings, industrial processes, and heat engines. That energy is used to perform functions that keep us warm in winter and cool in summer, keep foods cold, cook meals, run our computers, power our kitchen appliances and TV, and generally make our lives more enjoyable.
Thermodynamics is the science devoted to the study of energy and its transformations within and between objects that contain large numbers of molecules. These are called macroscopic systems, which include all objects with a large enough number of molecules that our human eyes can see them without the use of microscopes.
Macroscopic stuff includes a range of sizes from (approximately) the size of the period at the end of this sentence to planets, stars, galaxies and beyond. The energy within macroscopic matter is called internal energy. This internal energy can generally be increased or decreased by the use of heating or cooling, or work processes.
Given the importance of internal energy, I define thermodynamics as: the science concerned with internal energy changes of macroscopic matter by heat, work, and mass transport processes. Although this is the essence of thermodynamics, in reading about thermodynamics, it is uncommon to see explicit references to internal energy. Nevertheless, only by appreciating internal energy do thermodynamics in general, and entropy in particular, become understandable.
In order to understand thermodynamics, it is helpful to know that some energy types are stored by particles and systems of particles, while other energy types are involved in the transfer of energy from place to place within a given system, and from system to system. Although energy is one of the most fundamental concepts in physics, it is an elusive beast that is difficult to pin down. Fortunately, we can say some very definite things about the properties of energy. First, there are a variety of stored energy forms. In what follows, I outline some of these. Energy transfers are discussed in the next essay.
• Kinetic Energy
Ktrans = ½ mv2
Speed is more important than mass. Doubling the mass doubles Ktrans, while doubling the speed quadruples Ktrans. Translational kinetic energy is stored by an object and is transported from place to place. A baseball with a mass of 0.145 kg, with speed 45 meters/second (about 101 mph) has kinetic energy 1.46 x 105 joules. This is only about 1/7 of the number of joules released in the digestion of a slice of bread.
If the ball spins, it has rotational kinetic energy, which depends on m and the ball's radius through the so-called moment of inertia I, and fast it spins ω, the standard formula being
Krot = ½ I ω2
Again the important point is that doubling the mass doubles Krot, while doubling the rotational speed quadruples Krot. Baseballs tend to spin as they translate, and possess both translational and rotational kinetic energy. Rotational kinetic energy is transported spatially if the object also has non-zero translational kinetic energy.
Now suppose a ball sits motionless on a tabletop, or the air in a room has no measurable flow. The molecules within the ball and the air molecules are still moving, but the collection of molecules does not have any net overall motion. This means that the centers of mass have zero velocity. The molecules within these systems move in seemingly random directions, and are impossible to see with the naked eye.
The total energy adds up to a meaningful quantity, which is the internal energy U, mentioned earlier. In actuality it is the average total energy because macroscopic systems typically exchange small amounts of energy with their surroundings; i.e., their energies fluctuate a bit:
U = Average total energy
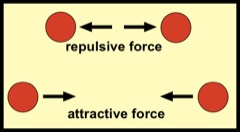
Consider two atoms or more generally, molecules, that repel (top row) or attract (bottom row) one another, depending upon how large their separation distance. At shorter distances they repel and at longer distances they attract. At one special intermediate separation distance, the force between them is zero.
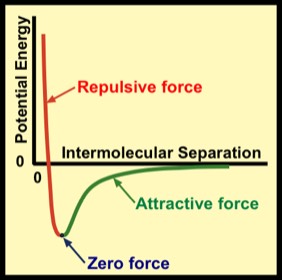
In summary, the force between the particles depends on the distance between them: a downward slope means the force is repulsive, and the more negative the slope the larger the force. An upward slope means it is attractive and the larger the slope, the larger the force. Zero slope simply means zero force. Notice that as the separation distance is increased in the green region, the curve's slope gets smaller, approaching zero; i.e., the force at sufficiently large distances becomes negligible.
By convention, the potential energy is defined such that it approaches zero in the limit of very large separation distances. With this definition, it turns out the the energy (kinetic plus potential) of a pair of particles that are bound to one another is a negative number. The interpretation is that it takes positive energy to break the bound unit into widely separated particles–e.g., the breaking of the water molecule, H20, into separated hydrogen and oxygen atoms.
The intermolecular potential energy and corresponding force is mainly electrostatic in nature; i.e., it is an electric force whose origin is a nonuniform charge distribution within each molecule. A pair of like charges; e.g., two electrons repel one another, while unlike charges; e.g., an electron and proton, attract. When atoms or molecules get sufficiently close together, the atomic electrons, which dominate the outer region of each particle get relatively close to one another. This can produce a substantial repulsive force.
Additionally, the Pauli exclusion principle encountered in studies of electrons in atoms, comes into play. It effectively keeps electrons from approaching one another, enhancing the effect of repulsion. This is not a force per se, as usually defined, but has an effect similar to a repulsive force.
Attractive forces are largely responsible for gases condensing to liquids, while repulsive forces make it increasingly difficult to compress gases and especially, liquids and solids to smaller volumes, Such compression brings particles closer together, and the repulsive forces become large.
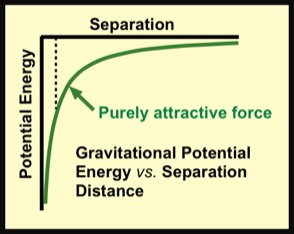
The potential energy between you and earth is also a mutual energy that is shared by earth and you. If you climb a mountain, as you get farther from earth’s center, the gravitational potential energy of the combination of earth and you increases. One way to think of this is that as you climb higher there is more potential for a fall to a lower altitude. Such a fall could would speed you up to a larger final speed for larger initial separation distances.
The gravitational force is responsible for earth's orbit around the sun and our moon's orbit around earth. As with molecules the total energy of a planet orbiting a star---namely, in a bound orbit---is negative. It takes positive energy to get the planet out of its orbit. More generally, the gravitational force plays a dominant role in the life-death patterns of stars, the evolution of galaxies, and cosmology generally.
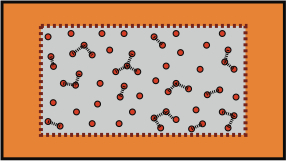
In a macroscopic thermodynamic system, which by definition has an enormous number of molecules, those molecules each have kinetic energies. These individual molecular energies, vary from instant to instant because of interactions with other molecules. Such interactions between pairs of molecules, especially those relatively close together, give rise to mutual potential energies, which also fluctuate with time. The sum of these many energy contributions is the total energy of the system. If the thermodynamic system were completely isolated from its surroundings, this total would be constant.
The figure shows a region of a gas, contained within the dotted boundary. Dashed lines between the closest pairs of molecules, connote the potential energies of largest magnitude. The main point is that both kinetic and potential energies contribute to the total system energy.
Because no thermodynamic system is totally isolated from its surroundings, energy exchanges between system and environment occur, and the total energy fluctuates from moment to moment. In thermodynamic equilibrium, these fluctuations are typically negligible relative to the total energy, and there is a well defined average energy. This is normally referred to as the system's internal energy.
• Photon Energy
As you know, the kinetic energy of a particle depends on its mass and speed. But not all "particles" have mass. Indeed, the constituents of electromagnetic (EM) radiation behave as particles that have zero mass! Indeed, the whole concept of a rest mass, namely the mass of an object at rest breaks down for EM radiation because there is no "rest frame." In vacuum, this radiation always moves at the same speed, the speed of light, c. And Einstein's theory of special relativity teaches us that no material object can reach this speed, so we cannot achieve the speed needed to have light appear to be at rest.
The light quanta postulated by Einstein have come to be called photons, the constituents of all EM radiation. They cannot be stopped and placed on a scale. They cannot speed up or slow down. Given this, we might expect all photons to carry the same energy, but this is not what Einstein found.
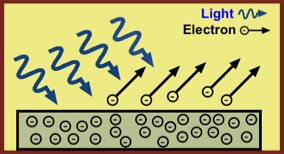
Einstein's work was published in the article, ""On a Heuristic Viewpoint Concerning the Production and Transformation of Light," for which he was awarded the Nobel Prize in physics in 1921. He showed that light can produce a photoelectric effect for a given metal if and only if its frequency f is high enough. Further, light travels in discrete bundles Einstein called light quanta, each of which carries energy
E = hf
Here, h is the fundamental physics constant called Planck constant, h = 6.64 x 10-34 Joule-seconds. It was not until 1926 that Gilbert Lewis coined the term photon for these light quanta. Although Lewis did this in the context of a model of a photon that fell by the wayside, the monicker photon stuck.
For our purposes, the mathematical details are unimportant. The important point here is that light travels in discrete quanta, photons. The energy of each photon is proportional to its frequency, which is an indicator of its color.
Corroboration of the frequency dependence is seen for an incandescent light bulb filament that is connected to a low electric voltage that is then slowly increased. The bulb's filament is heated by the electric current flowing through it. The very first color that appears when the filament begins to heat up is red, which is the lowest frequency light that the eye can see. As the filament gets hotter and hotter, the highest frequency light among the mix of frequencies that are emitted becomes orange, then yellow, green, blue and violet. When all these colors are being emitted, we interpret the resulting light as whitish. This is what we see when a light bulb is operated at the full design voltage, which is typically 120 Volts.
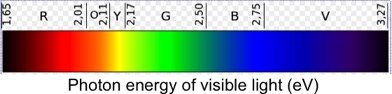
http://commons.wikimedia.org/wiki/File:Colors_in_eV.svg
A notable fact about the photoelectric effect is that if the incoming light does not have a sufficiently high frequency, there will be no emission of electrons. This is true no matter how intense the light is—i.e., how many photons arrive on the metal's surface each second. Only for sufficiently high-frequency light will electrons be ejected from a metal. Wikipedia has a table of the photon energy, in electron volts (eV), needed to eject electrons from more than 60 metals. (One eV is a very tiny amount of energy: 1 eV = 1.6 x 10-19 joules. This is the kinetic energy an electron would have if it were accelerated from rest, through a one volt electric potential difference; thus the name electron volt.) The lowest energy among the listed metals is about 2.1 eV, with most metals requiring 3.5 to 5.5 eV. As the figure shows, these are in the blue to violet range. Thus, most metals require photons at the higher energy (and frequency) range of visible light for the ejection of electrons via the photoelectric effect.
• Nuclear Energy
Nuclear energy, as it sounds is an energy associated with the nuclei of atoms. The lightest element of all, hydrogen—sometimes written as 1H—typically has one proton and zero neutrons in its nucleus. I write "typically" because this is the most common form of hydrogen. But a small fraction of hydrogen nuclei, written as 2H, on earth have one neutron accompanying the one proton needed to identify it as hydrogen. The resulting nucleus is sometimes referred to as a deuteron (for two "nucleons"—connoting protons and neutrons generally—in its nucleus), and a collection of such atoms is deuterium. Water containing this so-called heavy isotope of hydrogen is called heavy water. Another isotope of hydrogen is tritium, written as 3H. Note that the superscript is the number of protons plus neutrons—i.e., the number of nucleons. All atoms that have two or more protons in their nuclei also have some number of neutrons accompanying them.
To be clear, each element's name is based on the number of protons in its nucleus, and for each element, atoms with the same number of protons but differing numbers of neutrons are called isotopes. This is all relevant to energy because a strong nuclear force binds protons to neutrons at ultra-small separation distances—roughly of size 10-15 meters or less.
Associated with the binding of nucleons is a binding energy. This energy can be viewed as negative, in that a positive energy is needed to unbind one or more nucleons. It turns out that for lighter elements—actually those up to iron—the binding energy per nucleon becomes more negative as the elements get heavier. That means, for example, a deuteron can combine with another deuteron to free a proton and produce a heavier isotope of hydrogen called tritium:
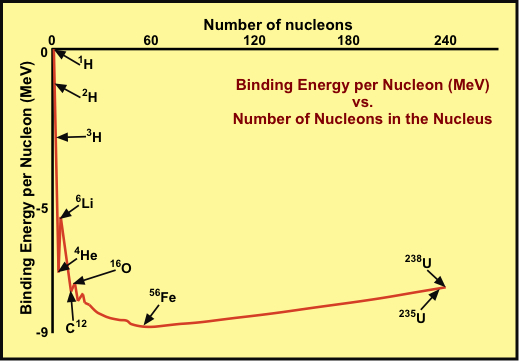
The graph shows the nuclear binding energy per nucleon as a function of the number of nucleons in the nucleus. For 1H, the binding energy is zero. It becomes stronger (more negative) for deuterium, 2H and tritium, 3H, and is stronger yet for 4He. The binding energy is strongest for 56Fe (iron) and is progressively weaker for heavier or lighter nuclei.
An important consequence of this is that nuclear fusion, with a release of energy is possible for nuclei lighter than iron, while nuclear fission, with a release of energy, is possible for nuclei heavier than iron. A prime example of fission occurs with uranium, the heaviest stable nucleus. Fission yields lighter nuclei with lower binding energies, and energy is released in the form of kinetic energy of the products. Fusion yields heavier nuclei with lower binding energies and, again, energy is released as kinetic energy.
An example of fusion is the collision of two deuterons (2H), yielding a triton and proton, each with significant kinetic energy. This is shown on the accompanying figure.
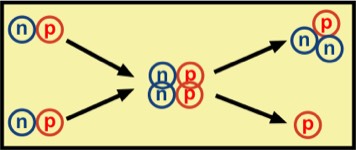
deuteron + deuteron
→ triton + proton
+ kinetic energy (of triton and proton)
(1 proton, 1 neutron) + (1 proton + 1 neutron) → (1 proton, 2 neutrons) + (1 proton)
Energy is conserved and the triton, with 1 proton and 2 neutrons, has lower binding energy than the sum of binding energies for the two initial deuterons. This decrease of energy is compensated primarily by the kinetic energy of the released neutron. This is an example of nuclear fusion, which is ubiquitous in stars, whose fuel is mainly hydrogen. This is expected for sufficiently young to medium age stars that have lots of hydrogen fuel available.
In 1905, Albert Einstein showed an "equivalence" between energy and mass using his special theory of relativity. The famous equation related to this is
E = mc2
This means that a particle of mass m has an energy E associated with it. The symbol c is the speed of light, which is 3 x 108 meters/second. Given the discussion above about deuteron-deuteron fusion to form a more tightly bound triton (more negative, thus lower binding energy), a consequence of Einstein's work is that
mdeuteron + mdeuteron > mtriton + mproton
The point is that the triton plus proton have lower binding energy and lower mass. Because energy is conserved this drop in energy must be accompanied by a gain of energy elsewhere. This is the kinetic energy of the triton and proton. Of course, the free proton on the right has zero binding energy. Putting known numbers into the left and right sides of the latter inequality, I find this:
Left side:
(3.34358348 + 3.34358348) x 10-27 kg = 6.68716696 x 10-27 kg
Right side:
(5.00735630 + 1.67262178) × 10−27 kg = 6.67997808 x 10-27 kg
This shows that the right side is indeed less than the left side. The "mass defect"—i.e., final mass minus initial mass—is -0.00718888 x 10-27 kg. If we multiply the the mass defect's magnitude by c2, we get 6.469992 x 10-13 Joules. This is the amount of energy that is released in the process. Using the common unit MeV (million electron volts), 4.04 MeV becomes kinetic energy.
To navigate to Energy Transfers, click HERE.